Modelo de Wolfram

En abril de 2020 el matemático, físico y científico Stephen Wolfram hizo una publicación sorprendente y potencialmente revolucionaria. Una nueva manera de explicar el universo que comprendería la totalidad de los fenómenos del cosmos, prometiendo unificar la física cuántica y la teoría de la relatividad. Lo que nos lleva a considerar la física de Wolfram como la posible teoría del todo.

a = a + 1

Teniendo conocimientos de álgebra notarás que esta ecuación no tiene sentido, pero sólo descubriendo cómo puede tener sentido, podremos entender el modelo que propone Wolfram.

La física clásica siempre ha usado ecuaciones para explicar el mundo. Fuerza es igual a masa por aceleración o la energía es igual a la masa por la velocidad de la luz al cuadrado.

F = m*a
E = m*c2

Es un modelo que funciona pero siguiendo es al logíca a = a + 1 no sería posible. Eso es porque no estamos hablando de una equivalencia, congelada en el tiempo, sino una regla o instrucción: Un algoritmo similar a un programa de ordenador:

si al inicio el valor de “a” era cero, al ejecutar el programa por primera vez, “a” será igual a uno. En el segundo turno, será igual a dos y así seguirá aumentando de valor mientras el programa siga ejecutandose. Si lo ejecutamos mil veces, sabemos que el valor de “a” será igual a mil. Si fuera un juego, sería muy sencillo y podemos predecir sus resultados. Pero hay juegos más complejos, como los llamados autómatas celulares, en los que reglas sencillas dan resultados asombrosos. Un ejemplo es el llamado “juego de la vida”, la idea es representar una cuadrícula. Cada casilla es una célula que tiene dos estados viva o muerta. El sistema está regido por unas reglas sencillas:

• Una célula muerta que tenga exactamente tres células vecinas vivas, nace, o sea que al turno siguiente estará viva.
• Una célula viva con 2 o 3 células vecinas vivas seguirá viva.
• Cualquier otra cantidad de células vecinas vivas, matará a la célula por sobrepoblación, o por soledad

Dadas estas reglas y dependiendo de la posición inicial se pueden obtener estructuras que se estabilizan, otras que se mueven en patrones cíclicos, o que evolucionan de maneras curiosas e incluso alunas que parecen estar vivas. Este tipo de estructuras son sistemas emergentes o autorganizados. Ya desde 2002 Wolfram propuso que era necesario usar estos sistemas para modelar y entender la complejidad del universo pero no era suficiente una rejilla bidimensional de cuadrados para modelar el cosmos.

El Proyecto de Física de Wolfram se presentó 18 años después, proponiendo el modelo de los hipergrafos. Todo empezó en 1736 en Königsberg. Esta ciudad tiene un río que la divide en cuatro partes, y 7 puentes que las comunican. Se plantó una cuestión: ¿Es posible visitar las cuatro partes de la localidad pasando por todos los puentes sólo una vez y volver al punto de partida? Este problema llegó al genio matemático Leonhard Euler que decidio representarlo con un diagrama: un grafo.

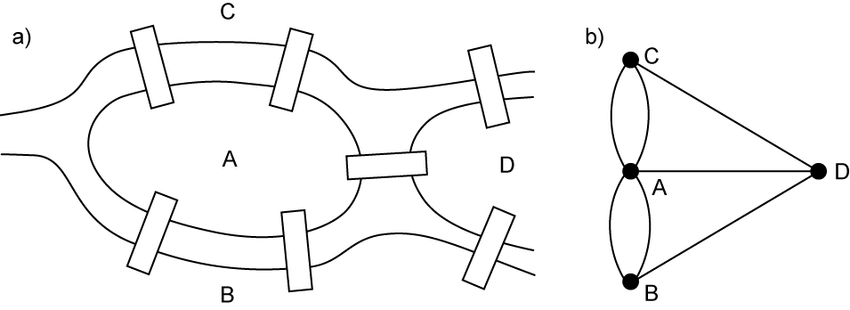
Cada punto es un nodo o vértice y cada línea una arista. Con este grafo se pudo resolver el problema: no es posible. De paso inventó la teoría de grafos que sirve para representar no sólo puentes, sino que además tiene muchas aplicaciones en la optimización de recorridos, procesos, flujos y sobre todo en informática, como los algoritmos de búsquedas.

El modelo de Wolfram usa, en vez de una retícula, la evolución de grafos, donde dadas ciertas reglas, el estado de los grafos cambia con cada “turno”.

El tiempo no tiene existencia independiente: es el transcurso de un estado a otro, y su unidad mínima es cada turno. La duración de cada turno es tan pequeña que a simple vista parece que el tiempo es continuo y que no tiene divisiones. El espacio tampoco existe como un lugar donde existe la materia; es simplemente el tamaño de la red de grafos. También está cuantizado, sus unidades mínimas son mucho más pequeñas que la partícula subatómica más pequeña conocida. La materia es el mismo espacio, pero enredado, serían nodos en el grafo agrupados de maneras específicas.

Una determinada red podría ser un protón, pero podría haber partículas mucho más pequeñas, llamadas oligones, que aunque tienen masa, serían indetectables y bien podría atribuírseles el papel de la materia oscura que tanto tiempo han buscado los astrofísicos. La energía, por su parte, es la acumulación de vértices en el eje del tiempo.

Un aspecto interesante del modelo es que es compatible con la relatividad: la aceleración se representa con una inclinación en el ángulo del hipergrafo, lo que da como resultado los efectos relativistas y, además, pone un límite a la velocidad: ningún efecto puede ocurrir antes que su causa: es la mayor inclinación que puede tener el grafo, el límite de la velocidad de la luz. En el modelo de Wolfram se representan los agujeros negros como regiones del grafo que evolucionan aparte del grafo principal. Y si esa rama evoluciona por su cuenta significa que está dando origen a un nuevo universo.

La física cuántica también tiene lugar. A diferencia del autómata celular, en el que dada
cierta regla se obtiene una historia única, el modelo de Wolfram incluye la reescritura de los grafos por sí mismos y la generación de árboles de historias, en las que varios estados existen con diferentes grados de probabilidad. El entrelazamiento cuántico, en el que dos partículas se comunican sus estados sin importar qué tan lejos estén, se explica como la consecuencia de que las partículas comparten un estado anterior en su historia. El modelo es complicado y difícil de entender, pero al mismo tiempo tiene una elegancia sencilla y práctica.

Afirmar que es una teoría del todo es precipitado. El proyecto de Wolfram, abierto a colaboradores, pretende generar una red hipergráfica que refleje las leyes de la física y encontrar así, en un futuro, cuáles son las instrucciones del programa y cuál es la regla original del universo. Lo que Wolfram propone no es una teoría, sino un cambio de paradigma. Una invitación a pensar la física de una manera diferente, lo que podría tener profundas implicaciones científicas, pero también filosóficas, al añadir el concepto del libre albedrío.

Este modelo tiene una propiedad llamada “irreductibilidad computacional”. En el ejemplo inicial es fácil saber con anticipación que, si ejecutamos el programa por doce mil turnos, “a” será igual que doce mil: es reductible y podemos reducir el resultado. Un programa como el de Wolfram es irreductible: no es posible tomar atajos y calcular por anticipado qué patrones o estructuras se formarán. Aunque el modelo es determinista, no hay nada predeterminado: es necesario ejecutar el programa, tomar decisiones y vivir esa historia para ver qué sucede.

---

Visita el canal de tutoriales de la Glitchcademia aquí.